经典算法之动态规划

动态规划

在众多算法中，动态规划在实际生活应用中算是比较常见的了，也是我们一定要掌握的一种算法，.

动态规划（dynamic programming， DP）是一种将复杂问题分解成更小的子问题来解决的优化技术。

不过动态规划和分治是不一样的，分治是把问题分解成相互独立的子问题，然后组合它们的的答案，而动态规划是将问题分解成相互依赖的子问题。

我们在这里引用三个经典的算法问题：

爬楼梯

爬楼梯算是动态规划最入门的一道题目了，很多公司的面试题甚至也有，先看题目：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 ：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

这道题目很多朋友一看就想到了斐波那契数列，然后就写出了代码：

var climbStairs = function(n) {
    return n < 3 ? n : climbStairs(n-1) + climbStairs(n-2);
};

这道题用这个其实是可以解出来的，但是时间复杂度是O(2^n)，你如果在LeetCode上提交会超时。

而动态规划的版本就可以让时间复杂度变为O(n):

var climbStairs = function(n) {
    let arr = [];
    for(let i = 1; i <=n; i++){
      if(i<3){
        arr[i - 1] = i;   // 先算出arr[3]和以下的值
      }else{
        arr[i-1] = arr[i-2] + arr[i-3]    // 无论是数字多大，它的答案都是由前一个和前两个的值相加的
      }
    }
    return n <= 0 ? 0 : arr[n-1]
};

这道题算是动态规划的入门题，但是也符合动态规划的核心理念。

背包问题

背包问题是最经典的算法题，无论是动态规划还是贪心算法都有，在动态规划中，我们遇到的是组合优化问题，题目一般是给定一个固定大小、能够携带重量W的背包，以及一组有价值和重量的物品，找出一个最佳解决方案，使得装入背包的物品总重量不超过W，且总价值最大。 我们假如有三个物品，它们分别的重量是2、3、4，价值分别是3、4、5，那么我们可以声明变量：

const values = [3,4,5],
weights = [2,3,4],
capacity = 5,
n = values.length;

接下来就是算法代码：

function knapSack(capacity, weights, values, n) {
  const KS = [];    // 初始化KS
  for (let i = 0; i <= n; i++) {
    KS[i] = [];   // 初始化矩阵
  }
  for (let i = 0; i <= n; i++) {
    for (let w = 0; w <= capacity; w++) {
      if (i === 0 || w === 0) {   // 第一行和第一列都为0
        KS[i][w] = 0;
      } else if (weights[i - 1] <= w) {   // 如果物品i的重量大于约束，直接赋值上一行的数值
        const a = values[i - 1] + KS[i - 1][w - weights[i - 1]];    // a的值为物品i的价值再加上上一行约束值减去物品i的重量值的价值
        const b = KS[i - 1][w];   // b的值为上一行的值
        KS[i][w] = a > b ? a : b;   // 取最大值
      } else {
        KS[i][w] = KS[i - 1][w]
      }
    }
  }
  return KS[n][capacity];
}

console.log(knapSack(capacity, weights, values, n))

可能代码的注释有些人看不懂，我上个图就知道了：

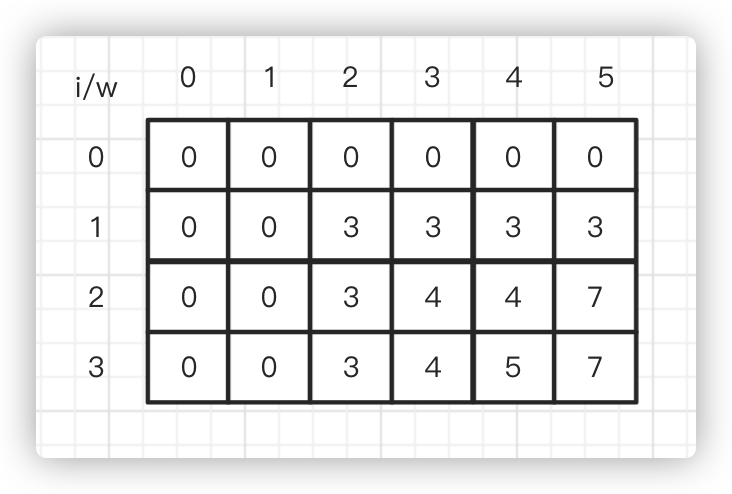
动态规划我一般习惯用二维数组来实现，当然，我们也可以用递归来实现：

function knapSack(capacity, weights, values, n) {
  if (n === 0 || capacity === 0) {
    return 0;
  }
  if (weights[n - 1] > capacity) {
    return knapSack(capacity, weights, values, n - 1);
  }
  const a = values[n - 1] + knapSack(capacity - weights[n - 1], weights, values, n - 1);
  const b = knapSack(capacity, weights, values, n - 1);
  return a > b ? a : b;
}

最长公共子序列

最长公共子序列也是动态规划问题的经典题目：找出两个字符串序列的最长子序列的长度。最长子序列是指，在两个字符串序列中以相同顺序出现，但不要求连续（非字符串子串）的字符串序列。

其实代码还是很简单的：

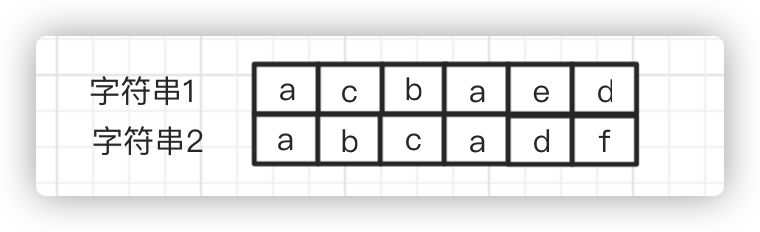
function lcs(wordX, wordY) {
  const m = wordX.length;
  const n = wordY.length;
  const l = [];

  for (let i = 0; i <= m; i++) {
    l[i] = [];  // 初始化矩阵
  }

  for (let i = 0; i <= m; i++) {    // 遍历两个字符串
    for (let j = 0; j <= n; j++) {
      if (i === 0 || j === 0) {
        l[i][j] = 0;    // 第一行和第一列全部赋值为0
      } else if (wordX[i - 1] === wordY[j - 1]) { 
        l[i][j] = l[i - 1][j - 1] + 1   // 如果相等那么上一行上一列的值加1
      } else {
        const a = l[i - 1][j];    // a的值为上一行的值
        const b = l[i][j - 1];    // b的值为上一列的值
        l[i][j] = a > b ? a : b   // 取较大的值
      }
    }
  }

  return l[m][n]
}

const wordX = 'acbaed';
const wordY = 'abcadf';
console.log(`lcs(wordX, wordY)`, lcs(wordX, wordY)) // 得出4

老规矩上图，其实这题跟上一条的背包问题差不多，都是最后的值是矩阵最右边最下边的。其实只要理解了为什么相等要取上一行上一列的值加1就理解了整个算法。

总结

无论是背包问题还是最长公共子序列，他们首先都要：

1. 定义子问题
2. 实现要反复执行来解决子问题的部分
3. 识别并求解出基线条件