用Javascript实现二叉搜索树（BST）

树的基本概念

树是一种分层数据的抽象模型，一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点（除了顶部的第一个节点）以及零个或多个子节点。

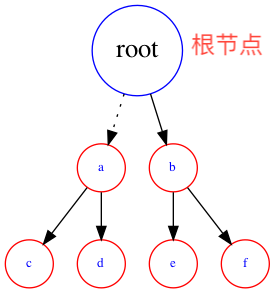
上面的树中，root就是根节点，而c、d、e、f是叶节点，叶节点是没有子元素的。

而这个树的深度是2，深度是由祖先节点来决定的，c的祖先节点有两个，所以深度是2。

树的高度取决于所有节点深度的最大值，所以是2。

这些都是树的基本概念，而后面我们将要讲二叉树和二叉搜索树。

二叉树和二叉搜索树（BST）

二叉树跟普通的树不一样的是二叉树中的节点最多只能有两个子节点：一个是左侧子节点，另一个是右侧子节点。

二叉搜索树（BST）则是二叉树的一种，但是只允许你在左侧节点存储比父节点小的值，往右侧节点存储比父节点大的值。如图所示：

代码实现

首先我们来创建节点的实现，每个节点需要一个类来表现：

class Node {
  constructor(key) {
    this.key = key;
    this.left = null;
    this.right = null;
  }
}

// 验证比较的函数
function defaultCompare(a, b) {
  if (a === b) {
    return 0;
  }
  return a < b ? -1 : 1;
}

left和right的作用和指针差不多，它们指向的也是一个Node节点。接下来我们来实现BST:

class BinarySearchTree{
  constructor(compareFn = defaultCompare) {
    this.compareFn = compareFn;   // 验证比较的方法
    this.root = undefined;    // 根节点
  }
}

插入值

insert(key) {
  if (this.root == null) {
    this.root = new Node(key);    // 如果没有根节点字直接初始化根节点
  } else {
    this.insertNode(this.root, key);
  }
}

insertNode(node, key) {
  if (this.compareFn(key, node.key) === -1) {   // 验证是否比此节点小
    if (node.left == null) {    // 如果左边没有节点则指向这个新节点，有的话传入左节点继续递归
      node.left = new Node(key);
    } else {
      this.insertNode(node.left, key);
    }
  } else if (node.right == null) {    // 右节点的处理跟左节点一样
    node.right = new Node(key);
  } else {    // 如果右节点有的话传入右节点继续递归
    this.insertNode(node.right, key);
  }
}

搜索值

我们如果要在二叉树中搜索一个值，那么我们就需要一个search方法：

search(key) {
    return this.searchNode(this.root, key);   // 初始的时候传入根节点
  }
searchNode(node, key) {
  if (node == null) {   // 如果这个节点是null直接返回false
    return false;
  }
  if (this.compareFn(key, node.key) === -1) {   // 如果小于当前比较的节点则传入左节点继续递归
    return this.searchNode(node.left, key);
  } else if (this.compareFn(key, node.key) === 1) {   // 如果大于当前比较的节点则传入右节点继续递归
    return this.searchNode(node.right, key);
  }
  return true;  // 直到最后返回true
}

最小值

我们如果要找找树的最小的值，可以通过下面的方法来实现：

min() {
  return this.minNode(this.root);   // 传入根节点
}
minNode(node) {
  let current = node;   // 循环查找节点，只要节点有左节点的就往左边查下去
  while (current != null && current.left != null) {   
    current = current.left;
  }
  return current;   // 没有左节点就返回当前节点
}

最大值

我们如果要找找树的最大的值，可以通过下面的方法来实现：

max() {
  return this.maxNode(this.root);   // 传入根节点
}
maxNode(node) {
  let current = node;   // 循环查找节点，只要节点有右节点的就往右边查下去
  while (current != null && current.right != null) {
    current = current.right;
  }
  return current;   // 没有右节点就返回当前节点
}

移除值

移除一个节点在树上是很复杂的，BST上实现这个方法其实逻辑不是很复杂，但是写起来就会很复杂：

remove(key){
  this.root = this.removeNode(this.root, key);
}

removeNode(node, key) {
  if (node == null) {
    return undefined;   // 如果节点不是有效的，返回undefined
  }
  // 需要删除的节点比当前节点小的时候，传入左节点递归
  if (this.compareFn(key, node.key) === -1) {
    node.left = this.removeNode(node.left, key);
    return node;
  // 需要删除的节点比当前节点大的时候，传入右节点递归
  } else if (this.compareFn(key, node.key) === 1) {
    node.right = this.removeNode(node.right, key);
    return node;
  }
  // 第一种情况就是要移除的节点没有左节点和没有右节点，直接把节点删除然后返回节点
  if (node.left == null && node.right == null) {
    node = undefined;
    return node;
  }
  // 第二种情况就是要移除的节点没有左节点或者没有右节点，那么就赋值那个有的那个节点到当前要移除的那个节点上
  if (node.left == null) {
    node = node.right;
    return node;
  } else if (node.right == null) {
    node = node.left;
    return node;
  }
  // 第三种情况就是要移除的节点有左节点和右节点，那么就需要找到它右节点中最小的子节点
  const aux = this.minNode(node.right);
  // 然后把找到的最小节点赋值后当前节点，并把它的指向更改为要移除的节点的右节点
  node.key = aux.key;
  // 这里需要注意为什么要递归，因为防止移除的节点的右节点的最小节点有子节点，所以需要递归来实现
  node.right = this.removeNode(node.right, aux.key);    
  return node;    // 返回节点
}

总结

这就是用JavaScript实现BST的过程，其实除了最后一个移除节点的方法比较难，其余的都是逻辑比较清晰简单。